1. Quelques définitions

Les différents types d’angles:

• angle aigu (inférieur à 90°)
• angle obtus (supérieur à 90°)
• angle droit (égale à 90°)
• angle plat (égale à 180°)
• angle saillant ( qui sort – « qui pique »)
• angle rentrant ( qui est vers l’intérieur de la figure)

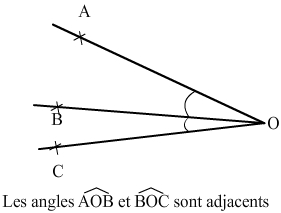
Les angles adjacents: ils sont un sommet et un coté commun. Ils sont situés de part et d’autre de la droite.

Les angles opposés par le sommet : ils ont en commun un sommet et leurs côtés sont dans le prolongement l’un de l’autre.

Deux angles opposés par le sommet sont égaux.

2. La bissectrice d’un angle

La bissectrice d’un angle est la droite qui passe par le sommet de l’angle et qui partage l’angle en 2 angles égaux.

Pour tracer la bissectrice d’un angle:

1. tracer avec le compas un arc de cercle de centre O qui coupe les droites en deux points : B et C
2. tracer deux arcs de cercle de même rayon de centre B et C qui vont se couper en D.
3. tracer la droite OD, on obtient la bissectrice de l’angle.

La bissectrice d’un angle est l’ensemble des points équidistants des côtés de cet angle.

La bissectrice d’un angle est aussi son axe de symétrie.

Les bissectrices des 3 angles d’un triangles sont toujours concourantes. Leur point commun est le centre d’un cercle tangent aux 3 côtés du triangle, c’est à dire le cercle inscrit dans le triangle.

Le centre du cercle inscrit est équidistant aux 3 côtés tangents à ce cercle .

3. Angles et droites parallèles.

Angles alternes- internes ou correspondants opposés par le sommet et définis à partir de droites parallèles ont même mesure.

Réciproque : si deux droites coupées par une sécante forme des angles alternes- internes ou égaux, alors ces droites sont parallèles.

Si un quadrilatère est un parallélogramme alors ses angles opposés ont même mesure et ses angles consécutifs sont supplémentaires (c’est à dire que la somme des angles est égale à 180°)

Angles alternes- externes :  ils sont situés de part et d’autre de la droite sécante des deux parallèles ; ils sont situés à l’extérieur des deux droites ; ils ne sont pas adjacents. Ils ont même mesure.

Réciproque: si deux droites coupées par une sécante forment des angles alternes-externes de même mesure, alors ces deux droites sont parallèles.

4. Angles et cercle

Angle au centre du cercle : angle dont le sommet est le centre du cercle, il intercepte l’arc.

Angle inscrit dans un cercle: angle dont le sommet est un point du cercle et les côtés coupent le cercle.

Si un angle AMB inscrit intercepte le même arc qu’un angle AOB au cercle alors AMB =1/2 AOB.

Si 2 angles inscrits interceptent le même arc alors ils sont égaux.

si [AB] est le diamètre du cercle C et M un point du cercle alors ABM est un triangle rectangle en M.

1. Droite, demi droite et segment

Droite (AB) ou (d)

Demie droite d’origine 1 passant par B [AB)

Segment [AB]

2. Cercle et disque

Le cercle de centre O et de rayon r est un ensemble de points situés à une distance identique r de O, r>0.

Le disque de centre O et de rayon r est un ensemble de points M tels que OM < ou = à r

C’est à dire que :

• si un point M est sur le cercle de centre O et de rayon r alors OM =r
• si un point M est tel que OM =r alors M est sur le cercle de centre O et de rayon r
• si A et B sont sur le cercle alors [OA]=[OB]=r et [AB] est le diamètre du cercle

3. Droites perpendiculaires

Les droites sont perpendiculaires si elles forment un angle droit (90°).

Si deux droites sont perpendiculaires, elles déterminent alors 4 angles droits.

Pour tracer un droite perpendiculaire
passant par un point (A) à une droite (d)

1. utiliser une règle et une équerre,
2. avec un compas et une règle:
   1. tracer un arc de cercle de centre A qui coupe une droite (d) en 2 points B et B’.
   2. tracer 2 arcs de cercle de centre B puis de centre B’ de même rayon et qui se coupent entre eux ( a l’opposé de A)
   3. la droite passant par A et par l’intersection des arcs de cercle de B et B’ est perpendiculaire à (d)

A noter qu’il n’y a qu’une seule droite passant par un point et perpendiculaire à une droite donnée.

La distance d’un point A a une droite (d) est la plus petite distance entre A et n’importe quel point de cette droite. Imaginons H la projection de A sur cette droite alors AH est perpendiculaire à (d)

Enfin quelque soit M appartenant à la droite (d), AMH est un triangle rectangle donc AM > AH

4. Droites parallèles (d)// (d’)

La distance entre 2 droites parallèles est constante.

2 droites perpendiculaires à une même droite (d) sont parallèles entre elles.

Pour tracer une droite parallèle à (une droite (d) passant par un point A:

1. placer 2 point B et B’ sur la droite (d).
2. tracer un arc de cercle de centre A et de rayon BB’ et un arc de cercle de centre B’ et de rayon AB.
3. la droite passant par A et par le point d’intersection des 2 arcs de cercles est parallèle à (d).

Démontrer que c’est une droite:

• Si AC+CB=AB alors A, B, C sont alignés
• si (AB) //(AC) alors A, B, C sont alignés.

5. Tangente à un cercle

Une tangente à un cercle est une droite qui a un seul point commun avec le cercle.

La tangente à un cercle de centre C, en un point M situé sur le cercle, est la droite perpendiculaire en M au rayon [CM]

6. Médiatrice d’un segment

La médiatrice d’un segment est l’ensemble des points équidistants des extrémités de ce segment.

La médiatrice est une droite qui est un axe de symétrie du segment. C’est la droite perpendiculaire à ce segment qui passe en son milieu.

Tracer la médiatrice d’un segment [AB]:

1. tracer 2 arcs de cercle de centre A et B qui se coupent en 2 points. Attention le rayon choisi doit être supérieur à AB/2.
2. tracer la droite joignant ses 2 points.

Propriétés:

1. si une droite est perpendiculaire à un segment et passe par son milieu alors c’est une médiatrice.
2. Si une droite est une médiatrice d’un segment alors elle est perpendiculaire à ce segment et passe par son milieu.
3. si un point est sur la médiatrice d’un segment alors il est équidistant des extrémités de ce segment et la réciproque est vrai. MA=MB.
4. si une droite passe par 2 points équidistants des extrémités d’un segment alors c’est la médiatrice de ce segment.
5. Si une droite passe par un point équidistant des extrémités et est perpendiculaire à ce segment alors c’est la médiatrice de ce segment.
6. La médiatrice d’un segment [AB] partage le plan en 2 demi plan Pa et Pb. Le demi plan Pa est l’ensemble des points M plus proche de l’extrémité A c’est-à-dire MA<MB. Le demi plan B c’est MB<MA.

7. Cercle circonscrit à un triangle

Le cercle circonscrit à un triangle est le triangle dans le cercle qui passe par les 3 sommets de ce triangle.

O est sur la médiatrice de [AB]. OA=OB. O est sur la médiatrice de AC donc OA=OC donc OA=OB=OC.

Le cercle de centre O et de rayon OA passe par les 3 sommets du triangle. De plus O est sur la médiatrice BC donc (AB), (BC) et (AC) sont concourantes en O.

La médiatrice d’un segment est l’ensemble des points équidistants des extrémités du segment.

Le centre du cercle circonscrit est équidistant des 3 sommets du triangle.