1. Étapes des apprentissages
- Construction de la notion: pour comparer et ordonner par la manipulation (faire des catégories, utiliser des baguettes, des ficelles, des bandelettes de papier, aider les élèves à faire la différence entre masse et volume.
- Additionner ou définir la somme puis construire un répertoire de référence.
- Introduction d’unité de mesure (donner du sens aux unités usuelles)
- Les unités de mesures usuelles (utilisation régulière).
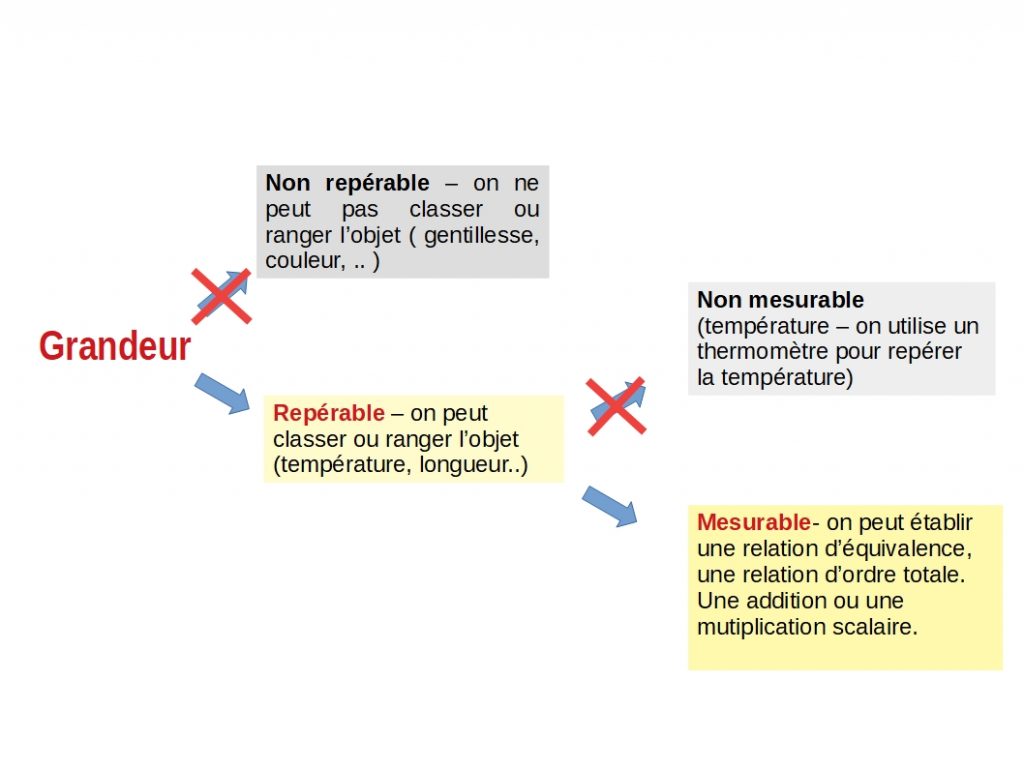
2. Les grandeurs enseignées.
La longueur est une grandeur définie par 2 relations: « à même longueur que » et » à une longueur plus grande que« .
L’aire est une grandeur définie pour les surfaces.
La masse est une grandeur qui caractérise les objets.
Le volume est une grandeur qui caractérise les solides.
3. La comparaison des grandeurs.
La comparaison sans mesurage est nécessaire pour les élèves non conservateurs et permet une différenciation au travers de la manipulation. En effet, il est possible de comparer de plusieurs manière:
- comparaison perceptive: à la vue, au soupesage des objets (à vue d’œil)
- comparaison directe: en juxtaposant les objets (les objets sont transportables)
- comparaison en utilisant un objet intermédiaire : utilisation d’un gabarit (les objets ne sont pas transportables), avec des objets intermédiaires que l’on peut couper et associer ou avec un compas pour reporter des longueurs.
- comparaison par transformation: comparer des longueurs de lignes brisés et des périmètres.
Difficultés/ erreurs des élèves:
- l’élève ne voit pas le lien entre le compas et la comparaison de la longueur (compas =cercle),
- l’élève applique les théorèmes en acte « la ligne brisée la plus longue est celle qui contient le plus de segments »,
- l’élève éprouve des difficultés de manipulations.
La comparaison en utilisant le mesurage c’est à dire en établissant un rapport entre la longueur à déterminer et les unités.
Difficultés/ erreurs des élèves:
- si ce rapport est un nombre entier inférieur à la longueur de l’instrument , l’élève place l’extrémité de sa règle sur le bout du segment à mesurer et non le zéro.
- si le rapport est un nombre décimal inférieur à la longueur de l’instrument:
- l’élève n’arrive pas à donner la mesure si ce n’est pas un nombre entier,
- l’élève fait une erreur de lecture des millimètres,
- l’élève a des difficultés de manipulations,
4. Au cycle 2
On vérifie l’addition des grandeurs (ajout de grandeurs).
On établit un répertoire de références pour estimer les mesures.
Effectuer des changements d’unités est une activité qui démarre au cycle 2 mais qui est largement développée au cycle 3 en prenant appui sur le tableau de conversion.
A retenir: MESURER permet de répondre numériquement à des problèmes de comparaison: définir des sommes, choisir un objet de référence comme unité, dénombrer combien d’unité. La comparaison est stable quelque soit l’unité.