1. Introduction
Il y a 4 situations possibles:
- la division partage (division partition, division quotition) cf. Vernguaud
- le rapport de 2 grandeurs de même nature. Comme π = P cercle/ Ø cercle
- le calcul d’une moyenne,
- la grandeur quotient associée à 2 grandeurs de natures différentes. Par ex: V= d/t (km/h)
La division de 2 nombres décimaux non entiers n »est pas étudié à l’école primaire => collège. Par contre on apprend la division décimale de 2 nombres entiers (CM1) et la division d’un nombre décimal par un entier (CM2).
2. Définition et propriétés
Dans N (les entiers naturels), la division avec reste est appelée division euclidienne: a = b x q + r
a est le dividende, b le diviseur, q le quotient et r le reste, il est toujours positif ou nul et TOUJOURS INFÉRIEUR à 0.
La division n’est ni commutative, ni associative. 1 est l’élément neutre tel que : a/1 = a
3. Progressivité des apprentissages
3.1 Au CE1
La compétence à construire et à acquérir pour le fin du CE1: approcher la division de 2 nombres entiers à partir d’un problèmes de partages ou de groupements. Partage par 2 et par 5.
Il est attendu que l’élève soit capable de :
- reconnaître un problème de « division », sachant que ce mot peut avoir deux sens:
- partage: basé sur le partgae du dividende par le diviseur. C’est celui qui est le plus vite reconnu par les élèves.
- groupement: basé sur la recherche du nombre de fois où le diviseur est contenu dans le dividende. Par exemple: combien de fois 2 dans 10
- dire que » dans une classe de 27 élèves on peut faire 5 équipes de 5 élèves et qu’il en reste 2″
- écrire 10 ÷ 2 = 2 ou 11 = (2 x 5) +1
En fin de CE1 l’élève doit reconnaître des situations de partage ou de groupements.
3.2 Au CE2
Compétences à construire et acquérir:
« Connaitre une technique opératoire de la division et la mettre en oeuvre avec un diviseur à un chiffre »
» Résoudre les problèmes de groupements et de partage: utiliser la division posée pour chercher le nombre de parts ou la valeur d’une part.«
Pour y parvenir:
- introduire l’idée de division en calcul mental par division exacte,
- étendre l’idée de division en calcul mental par division avec reste,
- entrainement avec des situations de partage puis de groupement, puis les 2 ensembles,
- faire émerger la nécessité d’utiliser une technique opératoire . Commencer par diviser un grand nombre par un petit et montrer la limite des procédures schématives, calcul mental, procédure additive, ..
- présenter la technique opératoire. En premier, on peut s’appuyer sur la procédure soustractive
- Réinvestir à travers des problèmes variés.
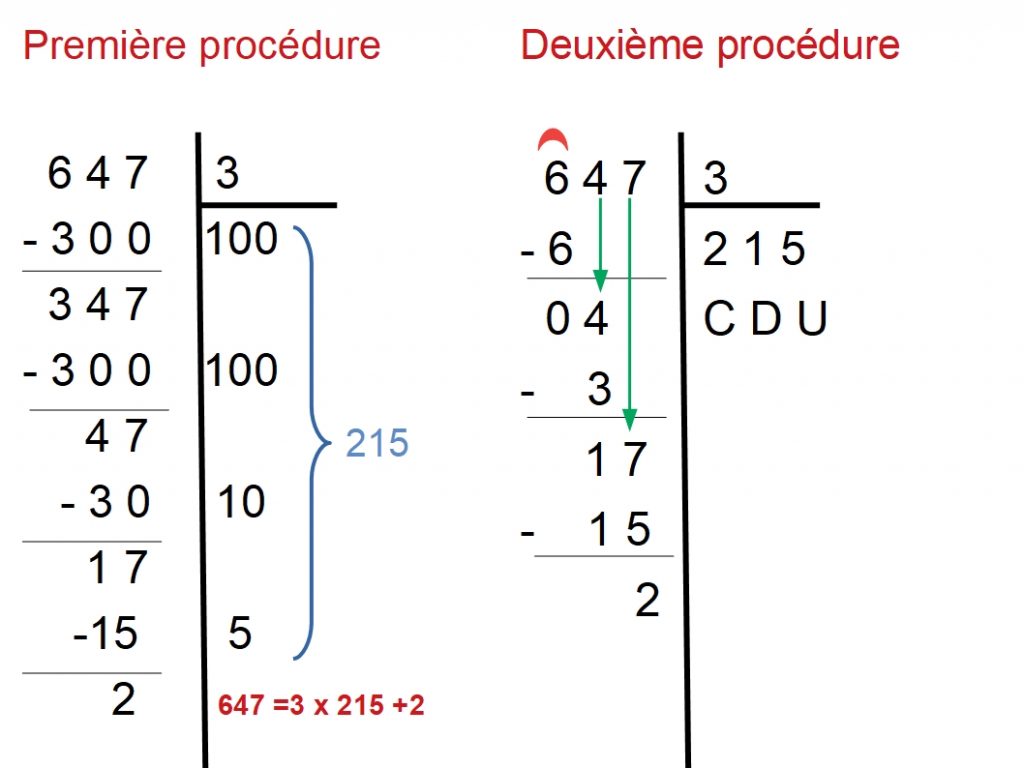
3.3 Au CM1
Compétences à construire et acquérir:
- » savoir poser/effectuer une division euclidienne de 2 entiers »
- » savoir poser et effectuer une division décimale de 2 entiers »
Pour ce faire, l’élève doit être capable de:
- maîtriser les 2 sens de la division : partage/groupement
- maîtriser les tables de multiplication
- connaitre la valeur de chaque chiffre selon sa position dans un nombre (entière, décimale, .)
- estimer le résultat ( encadrement, partage, …)
- mémoriser les résultats successivement obtenus
- vérifier/ contrôler le résultat.
3.3 Au CM2
Compétences à construire et acquérir:
- » savoir diviser un nombre décimal par un nombre entier »
4. Les difficultés.
La division est posée de gauche à droite.
Elle demande l’exécution simultanée de division, multiplication et soustraction.
La retenue peut être supérieure à 1 si la soustraction est partielle
5. Les erreurs
Mauvaises estimations des chiffres du quotient,
Mauvaise mémorisation des résultats,
Oubli d’un zéro,
Gestion du reste ou du diviseur.
6. Les connaissances
- repérage de la valeur des chiffres,
- les tables de multiplication,
- le calcul approché,
- le calcul de produits et de différences,
Merci beaucoup pour ce cours