Je vous mets le lien pour le pdf:
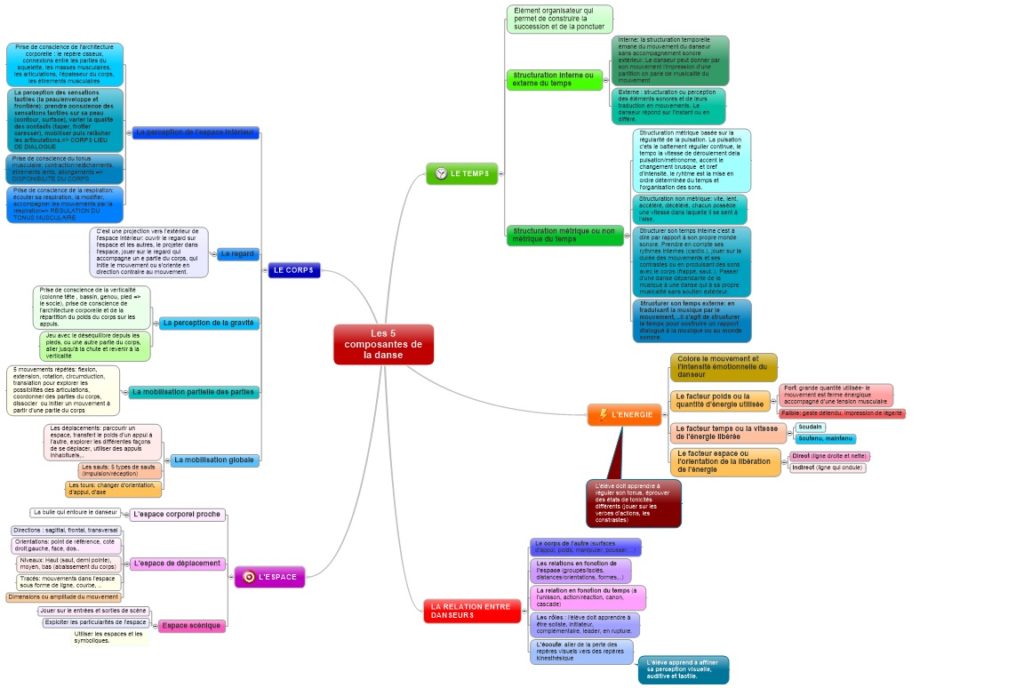
L’élève mobilise peu son corps=> il faut l’amener à développer un langage corporel varié en s’appuyant sur des images mentales ou l’utilisation de matériel.
L’élève utilise un espace limité (très fréquent) => développer toutes les directions en s’appuyant sur un balisage de l’espace, l’utilisation de l’imaginaire.
L’élève a toujours le même tempo, le même rythme => amener l’élève a être attentif au temps interne, proposer une évolution sans musique.
L‘énergie des mouvements est toujours égale => développer les sensations dues à l’énergie, en utilisant des dynamismes différents dans des jeux avec des actions soudaines.
L’élève « n’est pas dans sa danse » => développer l’attention et la concentration en instaurant une entrée dans l’activité dans la danse.
La séance se déroule ainsi :
Vous retrouverez à la fin de cet article 3 liens pour vous permettre d’approfondir ou de mieux comprendre ce qu’est la démarche de création en danse. Pour ma part je vous livre ici un petit résumé.
La démarche de création ce fait en plusieurs étapes:
Les liens qui vous serviront pour rentrer plus en détail dans le sujet:
https://web.ac-reims.fr/dsden10/exper/IMG/pdf/la_demarche_de_creation_en_danse_a_l_ecole.pdf
http://sylvain.obholtz.free.fr/cariboost_files/demcreation.pdf
Les ressources mobilisées par l’élève font directement écho aux enjeux ou attendus en danse.
Ressources affectives: il faut passer devant les autres, communiquer corporellement, connaitre ses possibilités gestuelles. Il arrive fréquemment qu’un élève refuse de s’engager en début de cycle de danse à cause de l’aspect émotionnel/ la difficulté de se laisser voir par les autres. Aussi, le passage de 2 groupes à la fois peut permettre de réduire cette « angoisse ».
Ressources motrices: l’élève doit maîtriser et utiliser les dissociations segmentaire, l’équilibre. Il développe une motricité expressive (contrôle son énergie).
Ressources informationnelles: l’élève doit prendre et anticiper les informations, faire des choix, se situer dans l’espace et le temps.
Ressources cognitives: imaginer, mémoriser, affiner son regard de spectateur
Ressources énergétiques: gérer son tonus pour maintenir la qualité de mouvement.