Dans la continuité de mon post d’hier soir, je me suis dit que j’allais vous parler des démonstrations. En effet, je m’appuie encore une fois sur le partiel que j’ai repassé avec l’amie en question.
L’exercice était à peu près de cet ordre là:
- Si le nombre choisi est 7 quel est la solution de cet algorithme?
- .. (j’ai oublié la question)
- Montrer que quelque soit le nombre impair choisi le résultat est multiple de 4 et carré d’un nombre.
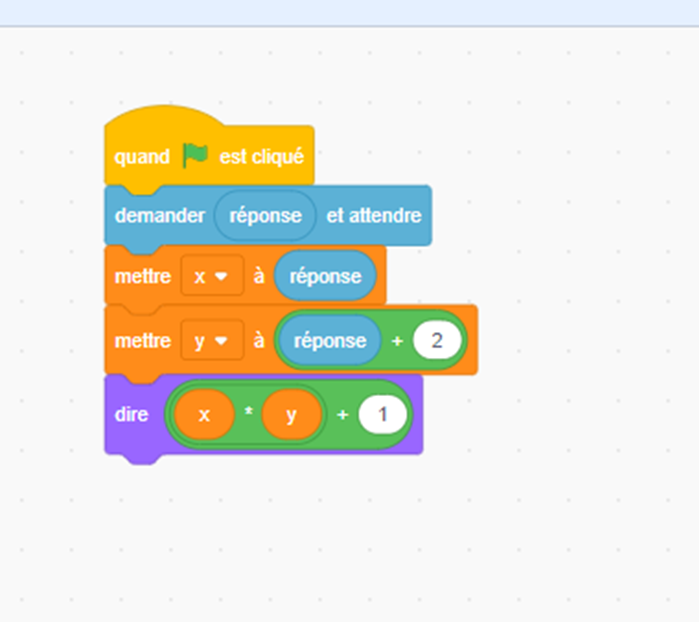
Pour résoudre la première question pas de problème, on suit l’algorithme sur scratch:
la réponse est 7
alors x=7 et y =7+2
donc x *y +1= 7 *(7+2)+1= 64
2…
3. Alors je rappelle ici un truc HYPER MAIS HYPER IMPORTANT au sujet des démonstrations
Pour montrer qu’une affirmation est fausse il suffit de trouver UN SEUL contre exemple.
Par contre, pour montrer qu’une affirmation est vrai alors il ne suffit pas de prendre 2 ou 3 exemple. Il faut prendre un cas général.
Si on dit que le nombre est impair alors on écrira soit n un nombre impair telque: n= 2k+1, k appartenant au entier naturel.
Pourquoi faire cette manipulation? Hé bien parce que en multipliant par 2 on est sur d’avoir un nombre pair et en lui ajoutant 1 on est sur que ça sera toujours un nombre impair comme résultat et ce quelque soit le nombre de départ choisi. Par exemple si k=5 alors n=11, si k=12 alors n=25
Donc dans notre cas n°1 n=7= 2*3+1
Si on exige un nombre pair alors on écrira n=2k (j’espère que vous n’êtes pas perdu)
Donc dans notre cas, à la question n°3, n=2k+1
n est la réponse que j’apporte à l’algorithme
alors x=n=2k+1
et y=n+2= 2k+1+2=2k+3
Alors
x*y+1= (2k+1)(2k+3)+1
= 2k*2k+2k*3+1*2k+1*3+1
=4k²+6k+2k+3+1
= 4k²+8k+4 ( je mets 4 en facteur)
= 4 (k²+2k+1) ainsi à ce stade on peut affirmer que le résultat est toujours un multiple de 4. Maintenant il faut reconnaître l’identité remarquable (a+b)²=a²+2ab+b²
=4 (k+1)² on démontre ici le résultat est toujours: et un multiple de 4 d’une part et le carré d’un entier d’autre part.